16th IAPR International Conference on
Discrete Geometry
for Computer Imagery
6-8 April 2011 Nancy, France
Demonstration Program (by submission order)
PDF version available here- 1. Sampling Surfaces and Volumes with Centroidal Voronoi Tesselations
- 2. Digital Geometry Tools and Algorithms Library
- 3. Interactive extraction of digital straight segments from gray-level images
- 4. Arc detection in linear time
- 5. Efficient Exact Computation for Incremental Discrete Rotation using Continued Fractino
- 6. Morphological and Discrete Geometry Operators in a Generic Image Processing Software Framework
- 7. Selection of relevant nodes from component-trees in linear time
- 8. Visualization of Discrete Geometry using the free and open-source software Sage
- 9. Circular arc reconstruction of digital contours with chosen Hausdorff error
- 10. Multiscale Analysis of Discrete Contours for Unsupervised Noise Detection
- 11. A near-linear time guaranteed algorithm for digital curve simplification under the Fréchet distance
- 12. A two-dimensional multi-scale discrete-Euclidean denoising/smoothing
- 13. Webcam filters in PureData for Art performance
- 14. Application of the mathematical morphology software Morph-M for image segmentation
Sampling is a fundamental operation that converts a continuous object into a discrete representation. Information theory provides some ways of characterizing the optimality of a discretization (quantization noise power). Centroidal Voronoi Tesselations are minimizers of the quantization noise power, and therefore can be used to compute an optimal discretization of an object. In this demo, we attempt to give an intuition of the mathematical concepts and algorithms to compute a Centroidal Voronoi Tesselation. Then we present several applications of Centroidal Voronoi Tesselations, to color quantization, meshing and remeshing in 2D and 3D. The demo will be presented using our Graphite software (alice.loria.fr/software/graphite) with a new technology that seamlessly integrates some slides and many software demonstrations. Some of the slides are available from: Some videos of the software that will be demonstrated can be seen from:
DGtal is a generic open source library for Digital Geometry programming whose main objective is to gather and structure different developments from the digital geometry and topology community. The benefits are numerous: to make easier the appropriation of our tools for a neophyte (new PhD students, researchers from other topics, ...), to permit better comparisons of new methods with already existing approaches, to construct a federative project. Furthermore we believe this is a necessary step for a better recognition of the efficiency of discrete geometry techniques by the important image analysis community. As a consequence, DGtal is designed so as to simplify the construction of effective demonstration tools. New results are thus easily shared to a vast audience.
On a more technical level, DGtal is developed in C++. Similarly to other classical libraries such as CGAL, it follows the paradigm of genericity with efficiency. This approach is made possible with the now well-known notion of concepts, implemented with templated types. The kernel of DGtal offers digital spaces of arbitrary dimension, with user-chosen integer types. Several digital topology algorithms are already implemented (Rosenfeld topology, connected components, simple points, homotopic thinning). The kernel manages generic images (standard raster images but also tree images), and arbitrary file formats with ImageMagick installed. Basic geometric primitives (digital lines and segments) are also available, as well as arbitrary dimensional volumetric distance transforms. A stream mechanism has been developed to display digital objects and export results in different vector formats.
DGtal is a collaborative effort --- for now --- of the French digital geometry community. It is still a work in progress but show already many promises to be the common basis for future developments made by the digital geometry community. The next milestone (DGCI) should include grid topology, geometric primitives and estimators, and other elements.
Visit the DGtal home page
Main participants:
D. Coeurjolly (LIRIS, Lyon), G. Damiand (LIRIS, Lyon), S. Fourey (GREYC, Caen), B. Kerautret (LORIA, Nancy), J.-O. Lachaud (LAMA, Chambéry), L. Provot (LORIA, Nancy), T. Roussillon (LIRIS, Lyon), I. Sivignon (Gipsa-lab, Grenoble).
 |
 |
 |
 |
(a) 3D homotopic thinning | (b) 2D euclidean distance transform | (c) Digital straight segment decomposition | (d) 2D image with a pointerless quadtree |
Many image processing applications rely on a man machine cooperation to select relevant visual features such as straight lines. In this demonstration, we present a new interactive method to select and extract straight lines from gray-level images. It is based on the concept of blurred segment used to bound noisy image data within thick segments with controlable width. Estimated position and direction parameters are refined through a three-steps coarse to fine approach. An incremental digital straight segment recognition algorithm has been extended to cope with gray-level information. It implements quite simple criteria to provide a restricted list of candidate pixels to the recognition process. This algorithm ensures compatible response time with man machine cooperation requirements.
A linear algorithm based on a discrete geometry approach is proposed for the detection of digital arcs and digital circles using a new representation of them. It is introduced by inspiring from the work of Latecki [Latecki00]. By utilizing this representation, we transform the problem of digital arc detection into a problem of digital straight line recognition. We then develop a linear method for the segmentation of curves into digital arcs. In addition, the proposed method can naturally work with disconnected or possibly noisy curves thanks to the notion of blurred segment [Debled05]. This simple and robust method can be applied to detect the arcs in images and technical documents.
(2) Université Paris-Est, Laboratoire d'Informatique Gaspard-Monge, Équipe A3SI, ESIEE Paris
We present an image processing framework centered on the Generic Programming paradigm in which an algorithm on the paper can be turned into a single code, written once and usable with various input types. The core of this project is a generic C++ library, Milena, which is part of a Free Software image processing platform, Olena. Milena can be used to implement algorithms on various data structures (subsets of Zn, graphs, cubical and simplicial complexes) and can be extended to support more data structures. We demonstrate the effectiveness of our approach by applying morphological and discrete geometry operators to various image types.
Component-trees associate to a discrete grey-level image a descriptive data structure induced by the inclusion relation between the binary components obtained at successive level-sets. This demonstration presents a software that performs an interactive segmentation of an image based on the concept of component-trees. The method is based on the extraction of a subset of the component-tree of an image enabling to fit at best a given binary target (manual marker) selected interactively in the image.
 |
 |
Outline of the method:
- [Step 1.] Interactive drawing of marker set.
- [Step 2.] Automatic computation of component-tree.
- [Step 3.] Interactive choice of $\alpha$ parameter, whiche defines the distance between marker set and component-tree nodes.
- [Step 4.] To refine the result: go to Step 1.
Since three years, I am using the software Sage to visualize and to do research in Discrete Geometry. Sage is great for its capacity of viewing objects in 2d (Matplotlib Python Library), 3d (Jmol, Tachyon and other 3d viewers) as well as its strong link with latex (the SageTex package). The code I developed allows to represent discrete planes, discrete lines and polyominoes with an approach based on combinatorics on words. For example, each figure of the paper "An Arithmetic and Combinatorial Approach to three-dimensional Discrete Lines" accepted in DGCI 2011 was generated using Sage code. The demonstration will give an idea of what can be done in Sage about Discrete Geometry. Sage is a free open-source mathematics software system licensed under the GPL. It combines the power of many existing open-source packages into a common Python-based interface. Its mission is to create a viable free open source alternative to Magma, Maple, Mathematica and Matlab. http://sagemath.org
slides [pdf] poster [pdf]
This demonstration presents a method of circular arc reconstruction given from a maximal Hausdorff error between the digital shape and its reconstruction. The method exploits the recent curvature estimators and the proposed algorithm approximate a digital shape with as few arcs as possible at a given scale, specified by a maximal admissible Hausdorff distance. We show the potential of our reconstruction method with numerous experiments and we also compare our results with some recent promising approaches. Last, all these algorithms are available online for comparisons on arbitrary shapes.
 |
 |
poster [pdf]
Blurred segments were introduced in discrete geometry to address possible noise along discrete contours. The noise is not really detected but is rather canceled out by thickening digital straight segments. The thickness is tuned by a user and set globally for the contour, which requires both supervision and non-adaptive contour processing. To overcome this issue, we propose an original strategy to detect locally both the amount of noise and the meaningful scales of each point of a digital contour. Based on the asymptotic properties of maximal segments, it also detects curved and flat parts of the contour. From a given maximal observation scale, the proposed approach does not require any parameter tuning and is easy to implement. This demonstration presents the detection of the meaningful scale through a on line demonstration website allowing to perform extraction on any gray level image.
 |
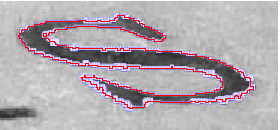 |
 |
slides [pdf] poster [pdf]
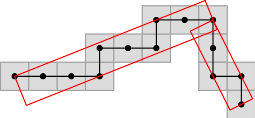
Given a digital curve and a maximum error, we propose an algorithm that computes a simplification of the curve such that the Fréchet distance between the original and the simplified curve is less than the error. Contrary to other classical metrics like L norms or Hausdorff distance, the Fréchet distance does not consider the curves as sets of points but takes into account the course of the curves. As a result, it nicely measures the similarity between two curves.
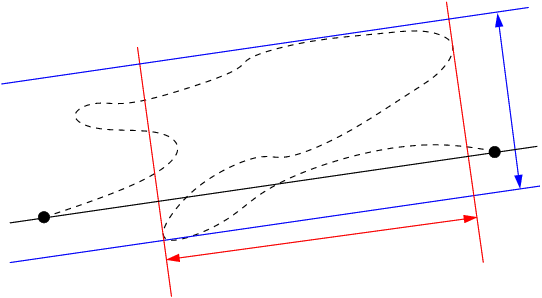
The algorithm uses an approximation of the Fréchet distance, but a guarantee over the quality of the simplification is proved. The algorithm is greedy and simply consists in defining shortcuts such that the distance between the shortcut and the curve is lower than the error. The approximation is based on the computation of two quantities: the width of the curve in the direction of the shortcut, and the length of the backpathes in this direction (see fig.1 (a)).
Even if the theoretical complexity of the algorithm is in O(n log(n)), experiments show a linear behaviour in practice. This demonstration is twofold: we propose a library written in C++ which implements the algorithm (see fig.2), and we also present an ipelet of this algorithm (to be used with the IPE drawing editor, see fig.1 (b)).
 |
 |
| (a) | (b) |
| Fig 1. (a) Illustration of the width and backpath length used in the approximated Fréchet distance. (b) A digital curve (red), its simplification with the approximated Fréchet distance (green) and its simplification using the width parameter only (blue). | |
 |
 |
| (a) | (b) |
| Fig 2. Result of the simplification algorithm on Plants images with an error equal to 6. | |
(2) LORIA, University of Nancy
(3) LAMA, University of Savoie
This demonstration presents a denoising and smoothing transform of two-dimensional discrete shapes. The transform consists of three steps: at first, a discrete contour analysis is performed. For each pixel of the shape contour, a meaningful scale (size) corresponding to the local nature on the contour is identified (see Demonstration 10). This scale is then used in the second step of the transform, as a scale parameter in an adaptive pixel size reconstruction. Finally, a digitization of the Euclidean reconstructed contour forms the last step of the proposed transform. This transform combines an adaptive denoising and a smoothing effect. We show with numerous experiments that this transform handles nicely most types of noise that may affect discrete shapes.
For pedagogical and artistic use, I have developed, together with Bilal Piot, a series of image filters that are applied in a real time pipeline fed by a webcam. The filters are based on mathematical concepts and help demonstrate notions like complex analytic functions, radius of convergence of a series, vector fields, ordinary differential equations, geometry of surfaces, Fourier transform, anamorphosis and tilings.
 |
 |
 |
 |
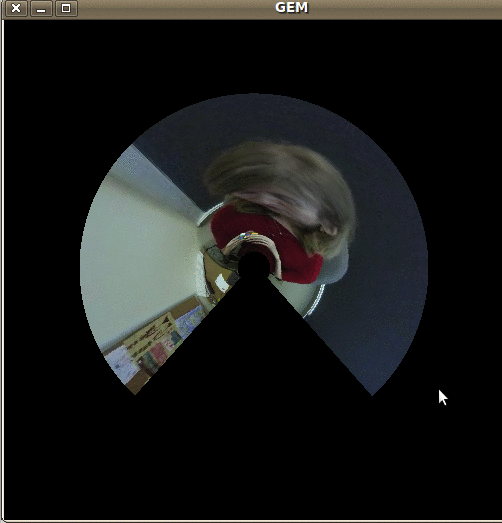 |
 |
Morph-M is an image processing library implemented on C++, following the principles of generic programming. This library contains most of the operators offered by mathematical morphology, from basic operations, such as dilations and erosions, up to the most powerful operators, such as the hierarchical watershed. The library also contains more classical functions of image processing.
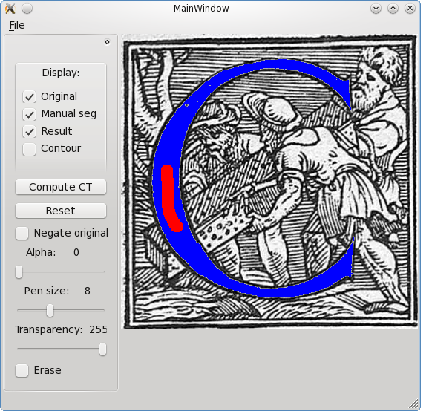
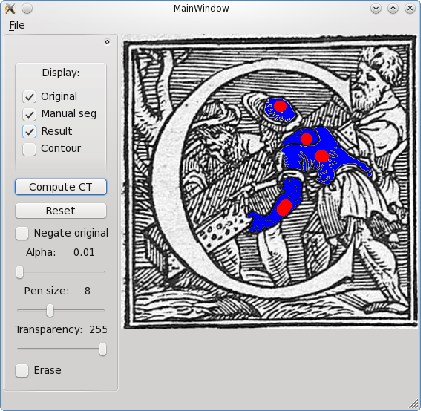
We present a simple graphical user interface dedicated to X-ray microtomographic images. Based on Morph-M, this software uses a graph-based version of the stochastic watershed to achieve a content-driven unsupervised segmentation.
The stochastic watershed segmentation was first introduced by Angulo and Jeulin in [1]. The approach is based on using a large number of realizations of random markers to build a probability density function (pdf) of contours, starting from a standard watershed algorithm producing oversegmentations. The stochastic watershed was proved to be efficient for unsupervised segmentation [2]. The two parameters used for its construction are K, the numbers of random markers used in each realization, and R, the numbers of realizations.
By construction, the pdf converges when increasing R. The parameter K needs to be proportional to the numbers of desired regions in the segmented image. Therefore, in the case of granular materials, K needs to be proportional to the number of grains contained in the image, that can be automatically estimated. In [2], the authors use the covariance for this estimation, deduced from the average radius of the grains, and a Boolean model assumption.
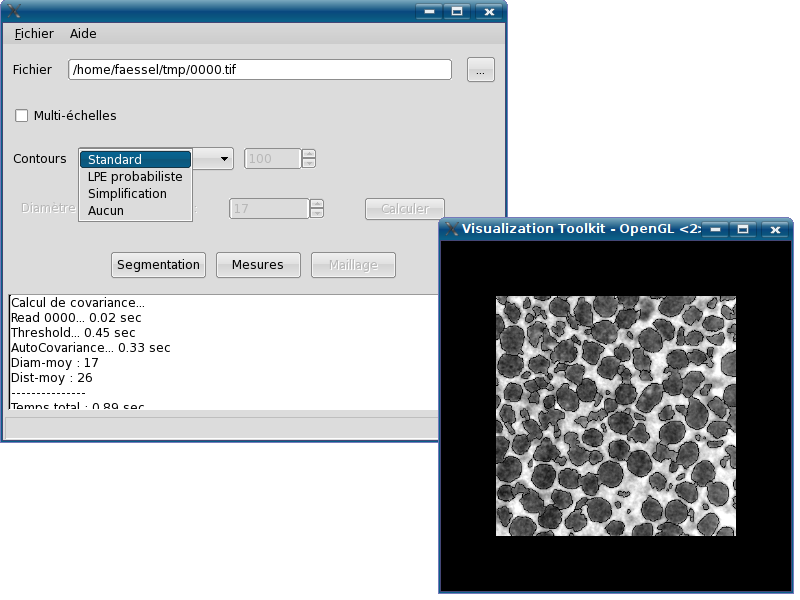
[2] Faessel, M., Jeulin, D.: Segmentation of 3D microtomographic images of granular materials with the stochastic watershed. Journal of Microscopy, Volume 239, Issue 1, 2010.


 Digital Geometry Tools and Algorithms Library
Digital Geometry Tools and Algorithms Library