Pursuing Explicit and Implicit Manifolds

by Information Projection

 

By Song-Chun Zhu (USA)

Reviewed by Aveek Shankar Brahmachari (USA)

Dr. Zhu started his talk by enlightening the audience with the need for a unified approach that can give the structure of the whole ensemble of generic natural images. He said that real world data are highly complex, non-Gaussian, and show high kurtosis. In his talk, he showed how pursuit of explicit and implicit manifolds by information projection can be done to yield the structure of the whole ensemble.

You can link to the presentation slides from the

ICPR 2008

web site

 

www.icpr2008.org/

 

or

click here

Dr. Zhu showed a wide spectrum of images of various categories from low to high entropy. Low and high entropy categories were seen containing less information. The middle entropy image category contains the most information. He suggests a unified framework to learn a probabilistic model on the space of image patches, intuitively governed by the above observation.

Image patches are fundamental elements for object recognition and modeling. Explicit manifold is a low dimensional, low entropy manifold spanned by image patches generated from the primitive model which involves hidden variables. Implicit manifolds are formed by image patches that share feature statistics. Implicit manifolds have high entropy. Implicit manifolds are specified by Markov Random Fields. Hidden variables for explicit manifolds and feature statistics for implicit manifold were suggested for the unified framework.

Kullback-Leibler divergence is used as negative log likelihood for pursuit of explicit and implicit manifolds. KL divergence is monotonically decreased by information projection to learn a probabilistic model on the space of image patches. Maximin learning principle was presented, claiming that it unifies other known visual modeling. This was followed by case studies and results.

Fig. 1  Showing image categories from low entropy to high entropy

Dr. Zhu concluded by talking about manifold transitions due to information scaling and summarized by recapitulating all the “ingredients of our herbs”:  two type manifolds, pursuit, integration, mixing, and transition.

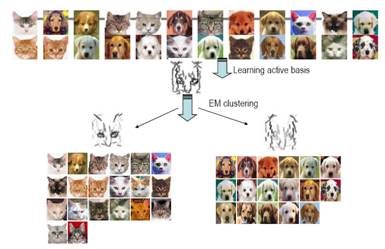
Fig.2 One of the result shown in Dr. Zhu’s talk

Return to Home Page